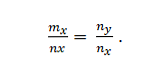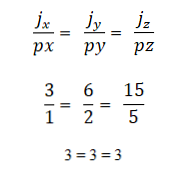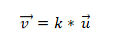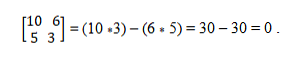Коллинеарность векторов
С 7‑го класса вы знакомы с такими физическими величинами, как сила, скорость, ускорение, перемещение, импульс. А что отличает их от другой группы величин, таких как длина, время, масса, объем, температура и плотность? Первая группа величин — векторные, то есть они характеризуются не только числовым значением, но и направлением. Нам важно знать не только скорость, но и ее направление; не только силу, с которой толкают груз, но и в каком направлении его толкают.
Ученики 9-го класса, помимо понятия вектора, должны знать, что такое коллинеарные векторы, а также условия коллинеарности векторов.
Вектор — это направленный отрезок. Вектор обозначается двумя заглавными латинскими буквами со стрелочкой над ними или одной маленькой со стрелочкой над ней .
Нулевой вектор — вектор, начало которого совпадает с концом. То есть в геометрической интерпретации это просто точка.
Теперь, когда мы вспомнили базовые понятия, можно переходить к определению коллинеарных векторов.
Что значит «коллинеарные векторы»
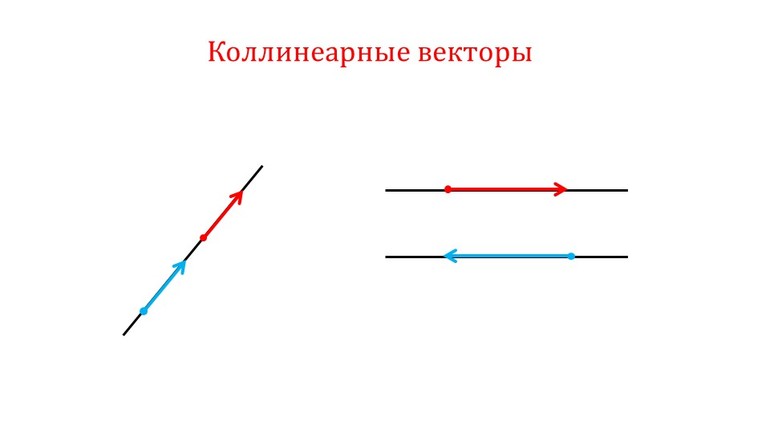
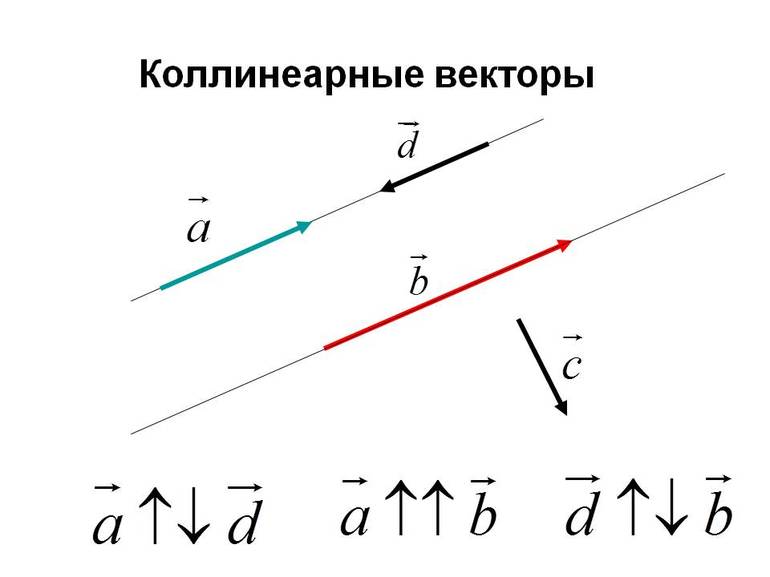
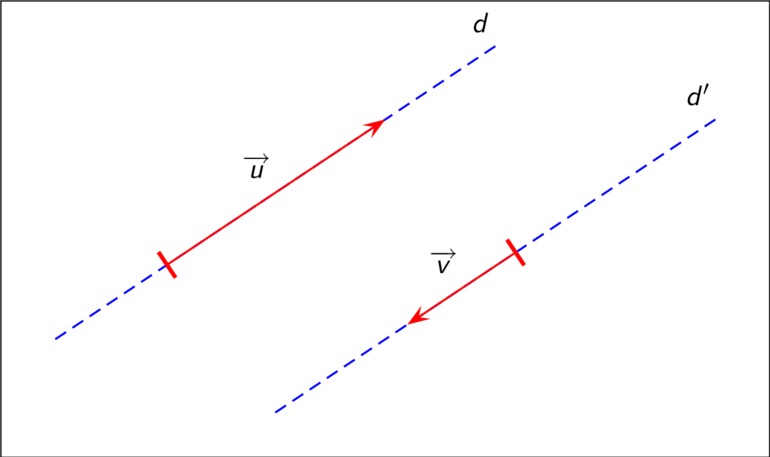
Коллинеарные векторы — это ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Причем считается, что нулевой вектор коллинеарен каждому другому вектору. То есть, попросту говоря, коллинеарность — это параллельность векторов. Если векторы и коллинеарны, то это записывают так: .
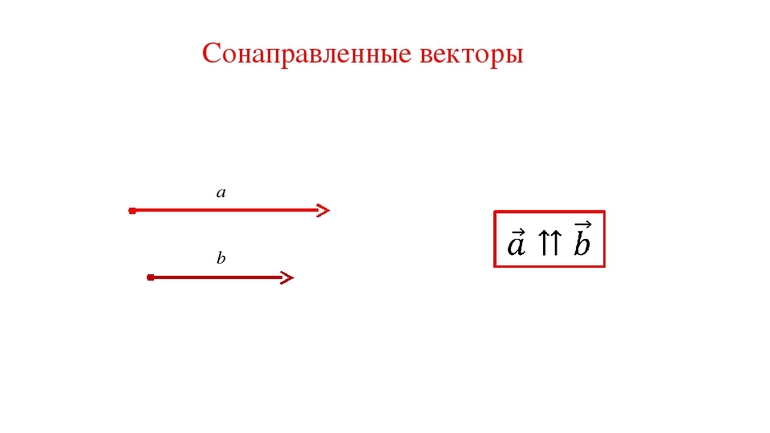
Коллинеарные векторы можно разделить по направлению на две группы: сонаправленные и противоположно направленные.
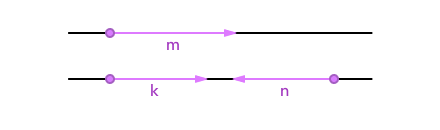
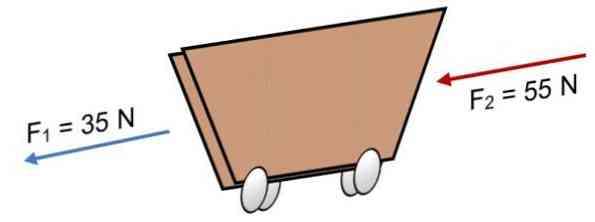
Векторы и лежат на параллельных прямых, а также имеют одно направление, поэтому и — сонаправленные векторы: .
Векторы и лежат на параллельных прямых, но имеют разное направление, поэтому и — противоположно направленные векторы: .
Задача № 1
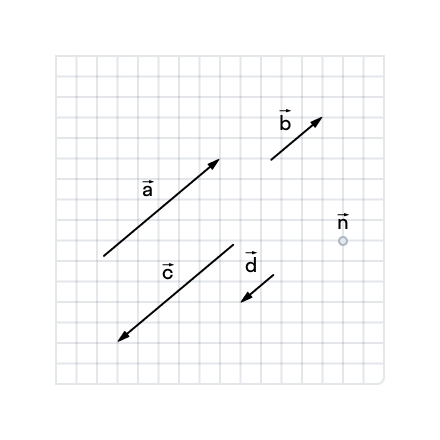
Найдите сонаправленные и противоположно направленные векторы.
Благодаря клетчатому фону мы можем определить, что все векторы на рисунке коллинеарны, то есть лежат на параллельных прямых. Осталось посмотреть на направление векторов и сделать выводы:
Но не забываем о нулевом векторе — он будет сонаправлен с каждым вектором.
Но согласитесь, что визуальная оценка параллельности не самая точная вещь на планете, а математика славится своей точностью и четкостью. Поэтому возникает вопрос: как проверить коллинеарность векторов алгебраическими способами? Для этого существуют признаки коллинеарности векторов. Рассмотрим их.
Признаки коллинеарности векторов
Первый критерий коллинеарности векторов: векторы и коллинеарны, если .
Второй критерий коллинеарности векторов: два вектора коллинеарны, если отношения их координат равны.
Но здесь важно понимать, что это условие параллельности векторов работает только для всех ненулевых координат. Значит, если хотя бы один компонент вектора равен нулю, то правило неприменимо.
Третий критерий коллинеарности векторов, который могут применять одиннадцатиклассники, взрослые и все, кто увлечен математикой: два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Применим условия коллинеарности векторов при решении задач.
Задача № 2
Докажите, что векторы и коллинеарны.
У нас с вами есть два способа определить или доказать коллинеарность векторов, однако в координатах каждого вектора есть нули — значит, подходит только первый критерий, который еще называется свойством коллинеарных векторов: если , то .
Для начала определим . А теперь проверим, выполняется ли условие :
, значит, . Что и требовалось доказать.
Задача № 3
Какие из векторов , и коллинеарны?
А здесь очень удобно использовать второй критерий коллинеарности векторов, который звучит так: отношения соответствующих координат коллинеарных векторов равны.
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — верно, значит, .
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.
Задача № 4
Определите, при каком значении k векторы и коллинеарны.
Так как по условию векторы должны быть коллинеарны, а в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности, а именно — должно выполняться условие , то есть .
По свойству пропорции выразим k:
Значит, при k = 27 векторы и коллинеарны.
Если же вам нужно проверить коллинеарность векторов в пространстве, а не на плоскости, то все эти условия продолжают работать, но помните, что к проверке присоединяется третья координата векторов. Рассмотрим пару примеров.
Задача № 5
Докажите, что векторы и коллинеарны.
Поступим аналогично решению в задаче 2 — применим первый критерий, который еще называется свойством коллинеарных векторов, т. е. если , то .
Для начала определим . А теперь проверим, выполняется ли условие :
, значит, . Что и требовалось доказать.
Задача № 6
Определите, при каких значениях k и f векторы и коллинеарны.
Аналогично задаче 4: так как по условию векторы должны быть коллинеарны и в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности. А именно — должно выполняться условие , то есть .
Рассмотрим первую и вторую дроби, по свойству пропорции выразим k:
Рассмотрим первую и третью дроби, по свойству пропорции выразим f:
Значит, при k = 27 и f = 2 векторы и коллинеарны.
Векторы — удивительная тема, с помощью которой можно решить многие физические задачи, легко и просто доказать самые сложные геометрические теоремы. Сегодня вы узнали, какие векторы называются коллинеарными, но это лишь один аспект большой главы о векторах. Чтобы узнать остальные действия с векторами, познакомиться с интересными задачами и способами решений, приходите на онлайн-курсы математики для детей в Skysmart.
Источник статьи: http://skysmart.ru/articles/mathematic/kollinearnost-vektorov
Коллинеарность – Collinearity
В геометрия, коллинеарность множества точек – это свойство их лежать на одном линия. [1] Набор точек с этим свойством называется коллинеарен (иногда пишется как коллинеарный [2] ). В более общем смысле этот термин использовался для выровненных объектов, то есть вещей, находящихся «в линию» или «в ряд».
Содержание
Очки на линии
В любой геометрии множество точек на прямой называется коллинеарен. В Евклидова геометрия это отношение интуитивно визуализируется точками, лежащими в ряд на «прямой линии». Однако в большинстве геометрий (включая евклидову) a линия обычно примитивный (неопределенный) тип объекта, поэтому такие визуализации не обязательно подойдут. А модель поскольку геометрия предлагает интерпретацию того, как точки, линии и другие типы объектов связаны друг с другом, и такое понятие, как коллинеарность, должно интерпретироваться в контексте этой модели. Например, в сферическая геометрия, где прямые представлены в стандартной модели большими окружностями сферы, а наборы коллинеарных точек лежат на одной большой окружности. Такие точки не лежат на «прямой линии» в евклидовом смысле и не считаются в ряд.
Отображение геометрии на себя, которое переводит линии в линии, называется коллинеация; он сохраняет свойство коллинеарности. В линейные карты (или линейные функции) из векторные пространства, рассматриваемые как геометрические карты, преобразовать линии в линии; то есть они сопоставляют наборы коллинеарных точек с наборами коллинеарных точек и, таким образом, являются коллинеатами. В проективная геометрия эти линейные отображения называются омографии и являются лишь одним из типов коллинеации.
Примеры в евклидовой геометрии
Треугольники
В любом треугольнике коллинеарны следующие множества точек:
- В ортоцентр, то центр окружности, то центроид, то Эксетер пойнт, то de Longchamps Point, а центр круг из девяти точек коллинеарны, все они попадают на линию, называемую Линия Эйлера.
- У точки де Лоншам также есть другие коллинеарности.
- Любая вершина, касание противоположной стороны с внеокружность, а Точка Нагеля коллинеарны в линии, называемой разветвитель треугольника.
- Середина любой стороны, точка, которая равноудалена от нее вдоль границы треугольника в любом направлении (так что эти две точки разрезать периметр пополам ), а центр круга Шпикера коллинеарны в линии, называемой тесак треугольника. (The Круг Шпикера это окружать из средний треугольник, и его центр это центр массы из периметр треугольника.)
- Любая вершина, касание противоположной стороны с вписанной окружностью и Точка Жергонна коллинеарны.
- С любой точки описанный круг треугольника, ближайшие точки на каждой из трех вытянутых сторон треугольника коллинеарны в Линия Симсона точки на описанной окружности.
- Линии, соединяющие ножки высоты пересекают противоположные стороны в коллинеарных точках. [3] : стр.199
- Треугольник стимулятор, середина высота, а точка контакта соответствующей стороны с внеокружность относительно этой стороны коллинеарны. [4] : стр.120, # 78
- Теорема Менелая заявляет, что три пункта п 1 , п 2 , п 3 < Displaystyle P_ <1>, P_ <2>, P_ <3>>
по бокам (некоторые расширенный ) треугольника против вершин А 1 , А 2 , А 3 < displaystyle A_ <1>, A_ <2>, A_ <3>>
соответственно коллинеарны тогда и только тогда, когда следующие произведения длин сегментов равны: [3] : п. 147
п 1 А 2 ⋅ п 2 А 3 ⋅ п 3 А 1 = п 1 А 3 ⋅ п 2 А 1 ⋅ п 3 А 2 . < Displaystyle P_ <1>A_ <2>cdot P_ <2>A_ <3>cdot P_ <3>A_ <1>= P_ <1>A_ <3>cdot P_ <2>A_ <1>cdot P_ <3>A_ <2>.>
- Инцентр, центроид и центр круга Шпикера коллинеарны.
- Центр окружности, Средняя точка Брокара, а Точка Лемуана треугольника коллинеарны. [5]
- Два перпендикулярные линии пересекаются на ортоцентр треугольника каждый пересекает каждый из треугольников расширенные стороны. Середины по трем сторонам этих точек пересечения коллинеарны в Линия Дроз – Фарный.
Четырехугольники
- В выпуклом четырехугольникABCD чьи противоположные стороны пересекаются в E и F, то средние точки из AC, BD, и EF коллинеарны, и линия, проходящая через них, называется Линия Ньютона (иногда известный как Линия Ньютона-Гаусса [нужна цитата ] ). Если четырехугольник тангенциальный четырехугольник, то на этой линии лежит и его инцентр. [6]
- В выпуклом четырехугольнике квазиортоцентр ЧАС, “центроид площади” грамм, а квазиокружный центр О коллинеарны в этом порядке, и HG = 2ИДТИ. [7] (Видеть Четырехугольник # Замечательные точки и прямые в выпуклом четырехугольнике.)
- Другие коллинеарности тангенциальный четырехугольник даны в Тангенциальный четырехугольник # Коллинеарные точки.
- В циклический четырехугольник, то центр окружности, то центроид вершины (пересечение двух бимедианов), а антицентр коллинеарны. [8]
- В круговом четырехугольнике центр тяжести площади, центр тяжести вершины и пересечение диагоналей лежат на одной прямой. [9]
- В тангенциальная трапеция, касания окружать с двумя основаниями коллинеарны центру.
- В тангенциальной трапеции середины ножек коллинеарны центру.
Шестиугольники
- Теорема Паскаля (также известная как теорема Hexagrammum Mysticum) утверждает, что если произвольные шесть точек выбраны на коническая секция (т.е. эллипс, парабола или же гипербола ) и соединены отрезками в любом порядке, чтобы сформировать шестиугольник, то три пары противоположных сторон шестиугольника (при необходимости удлиненные) встречаются в трех точках, лежащих на прямой линии, называемой линией Паскаля шестиугольника. Верно и обратное: Теорема Брейкенриджа – Маклорена утверждает, что если три точки пересечения трех пар прямых, проходящих через противоположные стороны шестиугольника, лежат на одной прямой, то шесть вершин шестиугольника лежат на конике, которая может быть вырожденной, как в Теорема Паппа о шестиугольнике.
Конические секции
- К Теорема Монжа, для любых трех круги в плоскости, ни одна из которых не находится полностью внутри одной из других, три точки пересечения трех пар прямых, каждая из которых касается двух окружностей, коллинеарны.
- В эллипс, центр, два фокусы, а два вершины с самым маленьким радиус кривизны коллинеарны, а центр и две вершины с наибольшим радиусом кривизны коллинеарны.
- В гипербола, центр, два фокуса и две вершины лежат на одной прямой.
Шишки
- В центр массы из коническое тело равномерной плотности лежит на одной четверти пути от центра основания до вершины на прямой, соединяющей их.
Тетраэдры
- Центроид тетраэдра – это середина между его Точка Монжа и центр окружности. Эти точки определяют Линия Эйлера тетраэдра, аналогичного Линия Эйлера треугольника. Центр сфера из двенадцати точек тетраэдра также лежит на прямой Эйлера.
Алгебра
Коллинеарность точек, координаты которых заданы
В координатная геометрия, в п-мерном пространстве, набор из трех или более различных точек коллинеарен тогда и только тогда, когда матрица координат этих векторов имеет вид классифицировать 1 или меньше. Например, учитывая три балла Икс = (Икс1, Икс2, . , Иксп), Y = (y1, y2, . , yп), и Z = (z1, z2, . , zп), если матрица
[ Икс 1 Икс 2 … Икс п y 1 y 2 … y п z 1 z 2 … z п ] < displaystyle < begin
имеет классифицировать 1 или меньше, точки лежат на одной прямой.
[ 1 Икс 1 Икс 2 … Икс п 1 y 1 y 2 … y п 1 z 1 z 2 … z п ] < displaystyle < begin
имеет классифицировать 2 или меньше, точки лежат на одной прямой. В частности, для трех точек на плоскости (п = 2), указанная выше матрица является квадратной, а точки коллинеарны тогда и только тогда, когда ее детерминант равно нулю; так как этот определитель 3 × 3 плюс или минус в два раза больше площадь треугольника с этими тремя точками в качестве вершин, это эквивалентно утверждению, что три точки коллинеарны тогда и только тогда, когда треугольник с этими точками в качестве вершин имеет нулевую площадь.
Коллинеарность точек, попарные расстояния которых заданы
Набор не менее трех различных точек называется прямой, что означает, что все точки коллинеарны тогда и только тогда, когда для каждых трех из этих точек А, B, и C, следующий определитель Определитель Кэли-Менгера равен нулю (с d(AB) означает расстояние между А и B, так далее.):
Det [ 0 d ( А B ) 2 d ( А C ) 2 1 d ( А B ) 2 0 d ( B C ) 2 1 d ( А C ) 2 d ( B C ) 2 0 1 1 1 1 0 ] = 0. < displaystyle det < begin
Этот детерминант определяется Формула Герона, равная −16 квадрату площади треугольника со сторонами d(AB), d(до н.э), и d(AC); поэтому проверка того, равен ли этот определитель нулю, эквивалентна проверке, есть ли у треугольника с вершинами А, B, и C имеет нулевую площадь (поэтому вершины лежат на одной прямой).
Эквивалентно, набор по крайней мере из трех различных точек коллинеарен тогда и только тогда, когда для каждых трех из этих точек А, B, и C с d(AC) больше или равно каждому из d(AB) и d(до н.э), неравенство треугольника d(AC) ≤ d(AB) + d(до н.э) выполняется с равенством.
Теория чисел
Два числа м и п не совмещать – то есть у них есть общий множитель, отличный от 1 – тогда и только тогда, когда для прямоугольника, нанесенного на квадратная решетка с вершинами в (0, 0), (м, 0), (м, п) и (0,п) хотя бы одна внутренняя точка коллинеарна (0, 0) и (м, п).
Параллелизм (плоский двойной)
В различных плоская геометрия понятие смены ролей «точек» и «линий» при сохранении связи между ними называется плоская двойственность. Учитывая набор коллинеарных точек, по двойственности плоскости мы получаем набор прямых, все из которых пересекаются в общей точке. Свойство, которым обладает этот набор линий (встреча в общей точке), называется параллелизм, и линии называются параллельные линии. Таким образом, параллелизм – это плоское понятие, двойственное коллинеарности.
График коллинеарности
Учитывая частичная геометрия п, где две точки определяют не более одной линии, a график коллинеарности из п это график чьи вершины являются точками п, где две вершины соседний тогда и только тогда, когда они определяют строку в п.
Использование в статистике и эконометрике
В статистика, коллинеарность относится к линейным отношениям между двумя объясняющие переменные. Две переменные идеально коллинеарен если между ними существует точная линейная зависимость, значит, корреляция между ними равна 1 или -1. То есть, Икс 1 < displaystyle X_ <1>> 



Икс 2 я = λ 0 + λ 1 Икс 1 я . < displaystyle X_ <2i>= lambda _ <0>+ lambda _ <1>X_ <1i>.>
Это означает, что если различные наблюдения (Икс1я, Икс2я ) нанесены в (Икс1, Икс2) плоскости эти точки коллинеарны в смысле, определенном ранее в этой статье.
Идеально мультиколлинеарность относится к ситуации, в которой k (k ≥ 2) объясняющие переменные в множественная регрессия модели идеально линейно связаны, согласно
Икс k я = λ 0 + λ 1 Икс 1 я + λ 2 Икс 2 я + ⋯ + λ k − 1 Икс ( k − 1 ) , я < displaystyle X_
для всех наблюдений я. На практике мы редко сталкиваемся с идеальной мультиколлинеарностью в наборе данных. Чаще проблема мультиколлинеарности возникает, когда существует «сильная линейная связь» между двумя или более независимыми переменными, что означает, что
Икс k я = λ 0 + λ 1 Икс 1 я + λ 2 Икс 2 я + ⋯ + λ k − 1 Икс ( k − 1 ) , я + ε я < displaystyle X_
Концепция чего-либо боковая коллинеарность расширяет эту традиционную точку зрения и указывает на коллинеарность между объясняющими и критериальными (т. е. объясненными) переменными. [10]
Использование в других областях
Антенные решетки
В телекоммуникации, а коллинеарная (или коллинеарная) антенная решетка является множество из дипольные антенны установлены таким образом, чтобы соответствующие элементы каждого антенна параллельны и выровнены, то есть расположены вдоль общей линии или оси.
Фотография
В уравнения коллинеарности представляют собой систему двух уравнений, используемых в фотограмметрия и компьютерное стереозрение, чтобы связать координаты в изображении (датчик ) плоскости (в двух измерениях) до координат объекта (в трех измерениях). В условиях фотографии уравнения выводятся с учетом центральная проекция точки объект сквозь оптический центр из камера к изображению в плоскости изображения (сенсора). Три точки, точка объекта, точка изображения и оптический центр, всегда коллинеарны. Другими словами, сегменты линии, соединяющие точки объекта с их точками изображения, совпадают в оптическом центре. [11]
Источник статьи: http://ru.wikial.top/wiki/Collinearity
Коллинеарность – Collinearity
В геометрия, коллинеарность множества точек – это свойство их лежать на одном линия. [1] Набор точек с этим свойством называется коллинеарен (иногда пишется как коллинеарный [2] ). В более общем смысле этот термин использовался для выровненных объектов, то есть вещей, находящихся «в линию» или «в ряд».
Содержание
Очки на линии
В любой геометрии множество точек на прямой называется коллинеарен. В Евклидова геометрия это отношение интуитивно визуализируется точками, лежащими в ряд на «прямой линии». Однако в большинстве геометрий (включая евклидову) a линия обычно примитивный (неопределенный) тип объекта, поэтому такие визуализации не обязательно подойдут. А модель поскольку геометрия предлагает интерпретацию того, как точки, линии и другие типы объектов связаны друг с другом, и такое понятие, как коллинеарность, должно интерпретироваться в контексте этой модели. Например, в сферическая геометрия, где прямые представлены в стандартной модели большими окружностями сферы, а наборы коллинеарных точек лежат на одной большой окружности. Такие точки не лежат на «прямой линии» в евклидовом смысле и не считаются в ряд.
Отображение геометрии на себя, которое переводит линии в линии, называется коллинеация; он сохраняет свойство коллинеарности. В линейные карты (или линейные функции) из векторные пространства, рассматриваемые как геометрические карты, преобразовать линии в линии; то есть они сопоставляют наборы коллинеарных точек с наборами коллинеарных точек и, таким образом, являются коллинеатами. В проективная геометрия эти линейные отображения называются омографии и являются лишь одним из типов коллинеации.
Примеры в евклидовой геометрии
Треугольники
В любом треугольнике коллинеарны следующие множества точек:
- В ортоцентр, то центр окружности, то центроид, то Эксетер пойнт, то de Longchamps Point, а центр круг из девяти точек коллинеарны, все они попадают на линию, называемую Линия Эйлера.
- У точки де Лоншам также есть другие коллинеарности.
- Любая вершина, касание противоположной стороны с внеокружность, а Точка Нагеля коллинеарны в линии, называемой разветвитель треугольника.
- Середина любой стороны, точка, которая равноудалена от нее вдоль границы треугольника в любом направлении (так что эти две точки разрезать периметр пополам ), а центр круга Шпикера коллинеарны в линии, называемой тесак треугольника. (The Круг Шпикера это окружать из средний треугольник, и его центр это центр массы из периметр треугольника.)
- Любая вершина, касание противоположной стороны с вписанной окружностью и Точка Жергонна коллинеарны.
- С любой точки описанный круг треугольника, ближайшие точки на каждой из трех вытянутых сторон треугольника коллинеарны в Линия Симсона точки на описанной окружности.
- Линии, соединяющие ножки высоты пересекают противоположные стороны в коллинеарных точках. [3] : стр.199
- Треугольник стимулятор, середина высота, а точка контакта соответствующей стороны с внеокружность относительно этой стороны коллинеарны. [4] : стр.120, # 78
- Теорема Менелая заявляет, что три пункта п 1 , п 2 , п 3 < Displaystyle P_ <1>, P_ <2>, P_ <3>>
по бокам (некоторые расширенный ) треугольника против вершин А 1 , А 2 , А 3 < displaystyle A_ <1>, A_ <2>, A_ <3>>
соответственно коллинеарны тогда и только тогда, когда следующие произведения длин сегментов равны: [3] : п. 147
п 1 А 2 ⋅ п 2 А 3 ⋅ п 3 А 1 = п 1 А 3 ⋅ п 2 А 1 ⋅ п 3 А 2 . < Displaystyle P_ <1>A_ <2>cdot P_ <2>A_ <3>cdot P_ <3>A_ <1>= P_ <1>A_ <3>cdot P_ <2>A_ <1>cdot P_ <3>A_ <2>.>
- Инцентр, центроид и центр круга Шпикера коллинеарны.
- Центр окружности, Средняя точка Брокара, а Точка Лемуана треугольника коллинеарны. [5]
- Два перпендикулярные линии пересекаются на ортоцентр треугольника каждый пересекает каждый из треугольников расширенные стороны. Середины по трем сторонам этих точек пересечения коллинеарны в Линия Дроз – Фарный.
Четырехугольники
- В выпуклом четырехугольникABCD чьи противоположные стороны пересекаются в E и F, то средние точки из AC, BD, и EF коллинеарны, и линия, проходящая через них, называется Линия Ньютона (иногда известный как Линия Ньютона-Гаусса [нужна цитата ] ). Если четырехугольник тангенциальный четырехугольник, то на этой линии лежит и его инцентр. [6]
- В выпуклом четырехугольнике квазиортоцентр ЧАС, “центроид площади” грамм, а квазиокружный центр О коллинеарны в этом порядке, и HG = 2ИДТИ. [7] (Видеть Четырехугольник # Замечательные точки и прямые в выпуклом четырехугольнике.)
- Другие коллинеарности тангенциальный четырехугольник даны в Тангенциальный четырехугольник # Коллинеарные точки.
- В циклический четырехугольник, то центр окружности, то центроид вершины (пересечение двух бимедианов), а антицентр коллинеарны. [8]
- В круговом четырехугольнике центр тяжести площади, центр тяжести вершины и пересечение диагоналей лежат на одной прямой. [9]
- В тангенциальная трапеция, касания окружать с двумя основаниями коллинеарны центру.
- В тангенциальной трапеции середины ножек коллинеарны центру.
Шестиугольники
- Теорема Паскаля (также известная как теорема Hexagrammum Mysticum) утверждает, что если произвольные шесть точек выбраны на коническая секция (т.е. эллипс, парабола или же гипербола ) и соединены отрезками в любом порядке, чтобы сформировать шестиугольник, то три пары противоположных сторон шестиугольника (при необходимости удлиненные) встречаются в трех точках, лежащих на прямой линии, называемой линией Паскаля шестиугольника. Верно и обратное: Теорема Брейкенриджа – Маклорена утверждает, что если три точки пересечения трех пар прямых, проходящих через противоположные стороны шестиугольника, лежат на одной прямой, то шесть вершин шестиугольника лежат на конике, которая может быть вырожденной, как в Теорема Паппа о шестиугольнике.
Конические секции
- К Теорема Монжа, для любых трех круги в плоскости, ни одна из которых не находится полностью внутри одной из других, три точки пересечения трех пар прямых, каждая из которых касается двух окружностей, коллинеарны.
- В эллипс, центр, два фокусы, а два вершины с самым маленьким радиус кривизны коллинеарны, а центр и две вершины с наибольшим радиусом кривизны коллинеарны.
- В гипербола, центр, два фокуса и две вершины лежат на одной прямой.
Шишки
- В центр массы из коническое тело равномерной плотности лежит на одной четверти пути от центра основания до вершины на прямой, соединяющей их.
Тетраэдры
- Центроид тетраэдра – это середина между его Точка Монжа и центр окружности. Эти точки определяют Линия Эйлера тетраэдра, аналогичного Линия Эйлера треугольника. Центр сфера из двенадцати точек тетраэдра также лежит на прямой Эйлера.
Алгебра
Коллинеарность точек, координаты которых заданы
В координатная геометрия, в п-мерном пространстве, набор из трех или более различных точек коллинеарен тогда и только тогда, когда матрица координат этих векторов имеет вид классифицировать 1 или меньше. Например, учитывая три балла Икс = (Икс1, Икс2, . , Иксп), Y = (y1, y2, . , yп), и Z = (z1, z2, . , zп), если матрица
[ Икс 1 Икс 2 … Икс п y 1 y 2 … y п z 1 z 2 … z п ] < displaystyle < begin
имеет классифицировать 1 или меньше, точки лежат на одной прямой.
[ 1 Икс 1 Икс 2 … Икс п 1 y 1 y 2 … y п 1 z 1 z 2 … z п ] < displaystyle < begin
имеет классифицировать 2 или меньше, точки лежат на одной прямой. В частности, для трех точек на плоскости (п = 2), указанная выше матрица является квадратной, а точки коллинеарны тогда и только тогда, когда ее детерминант равно нулю; так как этот определитель 3 × 3 плюс или минус в два раза больше площадь треугольника с этими тремя точками в качестве вершин, это эквивалентно утверждению, что три точки коллинеарны тогда и только тогда, когда треугольник с этими точками в качестве вершин имеет нулевую площадь.
Коллинеарность точек, попарные расстояния которых заданы
Набор не менее трех различных точек называется прямой, что означает, что все точки коллинеарны тогда и только тогда, когда для каждых трех из этих точек А, B, и C, следующий определитель Определитель Кэли-Менгера равен нулю (с d(AB) означает расстояние между А и B, так далее.):
Det [ 0 d ( А B ) 2 d ( А C ) 2 1 d ( А B ) 2 0 d ( B C ) 2 1 d ( А C ) 2 d ( B C ) 2 0 1 1 1 1 0 ] = 0. < displaystyle det < begin
Этот детерминант определяется Формула Герона, равная −16 квадрату площади треугольника со сторонами d(AB), d(до н.э), и d(AC); поэтому проверка того, равен ли этот определитель нулю, эквивалентна проверке, есть ли у треугольника с вершинами А, B, и C имеет нулевую площадь (поэтому вершины лежат на одной прямой).
Эквивалентно, набор по крайней мере из трех различных точек коллинеарен тогда и только тогда, когда для каждых трех из этих точек А, B, и C с d(AC) больше или равно каждому из d(AB) и d(до н.э), неравенство треугольника d(AC) ≤ d(AB) + d(до н.э) выполняется с равенством.
Теория чисел
Два числа м и п не совмещать – то есть у них есть общий множитель, отличный от 1 – тогда и только тогда, когда для прямоугольника, нанесенного на квадратная решетка с вершинами в (0, 0), (м, 0), (м, п) и (0,п) хотя бы одна внутренняя точка коллинеарна (0, 0) и (м, п).
Параллелизм (плоский двойной)
В различных плоская геометрия понятие смены ролей «точек» и «линий» при сохранении связи между ними называется плоская двойственность. Учитывая набор коллинеарных точек, по двойственности плоскости мы получаем набор прямых, все из которых пересекаются в общей точке. Свойство, которым обладает этот набор линий (встреча в общей точке), называется параллелизм, и линии называются параллельные линии. Таким образом, параллелизм – это плоское понятие, двойственное коллинеарности.
График коллинеарности
Учитывая частичная геометрия п, где две точки определяют не более одной линии, a график коллинеарности из п это график чьи вершины являются точками п, где две вершины соседний тогда и только тогда, когда они определяют строку в п.
Использование в статистике и эконометрике
В статистика, коллинеарность относится к линейным отношениям между двумя объясняющие переменные. Две переменные идеально коллинеарен если между ними существует точная линейная зависимость, значит, корреляция между ними равна 1 или -1. То есть, Икс 1 < displaystyle X_ <1>> 



Икс 2 я = λ 0 + λ 1 Икс 1 я . < displaystyle X_ <2i>= lambda _ <0>+ lambda _ <1>X_ <1i>.>
Это означает, что если различные наблюдения (Икс1я, Икс2я ) нанесены в (Икс1, Икс2) плоскости эти точки коллинеарны в смысле, определенном ранее в этой статье.
Идеально мультиколлинеарность относится к ситуации, в которой k (k ≥ 2) объясняющие переменные в множественная регрессия модели идеально линейно связаны, согласно
Икс k я = λ 0 + λ 1 Икс 1 я + λ 2 Икс 2 я + ⋯ + λ k − 1 Икс ( k − 1 ) , я < displaystyle X_
для всех наблюдений я. На практике мы редко сталкиваемся с идеальной мультиколлинеарностью в наборе данных. Чаще проблема мультиколлинеарности возникает, когда существует «сильная линейная связь» между двумя или более независимыми переменными, что означает, что
Икс k я = λ 0 + λ 1 Икс 1 я + λ 2 Икс 2 я + ⋯ + λ k − 1 Икс ( k − 1 ) , я + ε я < displaystyle X_
Концепция чего-либо боковая коллинеарность расширяет эту традиционную точку зрения и указывает на коллинеарность между объясняющими и критериальными (т. е. объясненными) переменными. [10]
Использование в других областях
Антенные решетки
В телекоммуникации, а коллинеарная (или коллинеарная) антенная решетка является множество из дипольные антенны установлены таким образом, чтобы соответствующие элементы каждого антенна параллельны и выровнены, то есть расположены вдоль общей линии или оси.
Фотография
В уравнения коллинеарности представляют собой систему двух уравнений, используемых в фотограмметрия и компьютерное стереозрение, чтобы связать координаты в изображении (датчик ) плоскости (в двух измерениях) до координат объекта (в трех измерениях). В условиях фотографии уравнения выводятся с учетом центральная проекция точки объект сквозь оптический центр из камера к изображению в плоскости изображения (сенсора). Три точки, точка объекта, точка изображения и оптический центр, всегда коллинеарны. Другими словами, сегменты линии, соединяющие точки объекта с их точками изображения, совпадают в оптическом центре. [11]
Источник статьи: http://ru.zahn-info-portal.de/wiki/Collinearity
Коллинеарность
В геометрии , коллинеарность множества точек является собственностью их лежащими на одной линии . [1] Набор точек с этим свойством называется коллинеарным (иногда пишется как коллинеарный [2] ). В более широком смысле этот термин использовался для выровненных объектов, то есть вещей, расположенных «в линию» или «в ряд».
Точки на линии
В любой геометрии множество точек на прямой называется коллинеарным . В евклидовой геометрии это отношение интуитивно изображается точками, лежащими в ряд на «прямой». Однако в большинстве геометрий (включая евклидову) линия обычно является примитивным (неопределенным) типом объекта , поэтому такие визуализации не обязательно будут уместны. Модель для геометрии предлагает интерпретацию того , как точки, линии и другие типы объектов связаны друг с другом и понятия , такие как коллинеарности должны быть интерпретированы в контексте этой модели. Например, в сферической геометрии , где линии представлены в стандартной модели большими кругами сферы, множества коллинеарных точек лежат на одном и том же большом круге. Такие точки не лежат на «прямой линии» в евклидовом смысле и не считаются расположенными в ряд .
Отображение геометрии на себя, переводящее линии в линии, называется коллинеацией ; он сохраняет свойство коллинеарности. Линейные карты (или линейные функции) векторных пространств , рассматриваемые как геометрические карты, отображают линии в линии; то есть они отображают наборы коллинеарных точек в наборы коллинеарных точек и, таким образом, являются коллинеациями. В проективной геометрии эти линейные отображения называются омографиями и представляют собой лишь один тип коллинеаций.
Примеры в евклидовой геометрии
Треугольники
В любом треугольнике коллинеарны следующие множества точек:
- Ортоцентр , центр описанной окружности, центр тяжести , точка Эксетера , точка де Лоншана и центр девятиточечного круга коллинеарны, и все они падают на линию, называемую линией Эйлера .
- Точка де Лоншана имеет и другие коллинеарности .
- Любая вершина, касание противоположной стороны с вписанной окружностью и точка Нагеля коллинеарны на линии, называемой разделителем треугольника.
- Середина любой стороны, точка, равноудаленная от нее вдоль границы треугольника в любом направлении (таким образом, эти две точки делят периметр пополам ), и центр круга Шпикера коллинеарны по линии, называемой секущей треугольника. ( Круг Шпикера — это вписанная окружность медиального треугольника , а его центр — центр масспериметра треугольника .)
- Любая вершина, касание противоположной стороны с вписанной окружностью и точка Жергонна коллинеарны.
- Из любой точки описанной окружности треугольника ближайшие точки на каждой из трех расширенных сторон треугольника коллинеарны линии Симсона точки описанной окружности.
- Линии, соединяющие основания высот , пересекают противоположные стороны в коллинеарных точках. [3] : стр. 199
- Центр треугольника , середина высотыи точка касания соответствующей стороны с вписанной окружностью относительно этой стороны лежат на одной прямой. [4] : стр.120, #78
- Теорема Менелая утверждает, что три точки п 1 , п 2 , п 3 <\ displaystyle P_ <1>, P_ <2>, P_ <3>>
на сторонах (некоторых расширенных ) треугольника, противоположных вершинам А 1 , А 2 , А 3 <\ Displaystyle А_ <1>, А_ <2>, А_ <3>>
соответственно коллинеарны тогда и только тогда, когда равны следующие произведения длин отрезков: [3] : p. 147
п 1 А 2 ⋅ п 2 А 3 ⋅ п 3 А 1 знак равно п 1 А 3 ⋅ п 2 А 1 ⋅ п 3 А 2 . <\ displaystyle P_ <1>A_ <2>\ cdot P_ <2>A_ <3>\ cdot P_ <3>A_ <1>= P_ <1>A_ <3>\ cdot P_ <2>A_ <1>\cdot П_<3>А_<2>.>
- Центр вписанной окружности, центр тяжести и центр круга Шпикера коллинеарны.
- Центр описанной окружности, середина Брокара и точка Лемуана треугольника лежат на одной прямой. [5]
- Две перпендикулярные линии, пересекающиеся в ортоцентре треугольника, пересекают каждую из расширенных сторон треугольника . Середины по трем сторонам этих точек пересечения коллинеарны на линии Дроз-Фарни .
Четырехугольник
- В выпуклом четырехугольникеABCD , противоположные стороны которого пересекаются в точках E и F , серединыAC , BD и EF лежат на одной прямой, а линия, проходящая через них, называется линией Ньютона ( иногда ее называют линией Ньютона-Гаусса ) . Если четырехугольник является касательным четырехугольником , то его центр вписанной стороны также лежит на этой прямой. [6]
- В выпуклом четырехугольнике квазиортоцентр H , «центроид площади» G и квазицентр окружности O коллинеарны в этом порядке, и HG = 2 GO . [7] (См. Четырехугольник # Замечательные точки и прямые в выпуклом четырехугольнике .)
- Другие коллинеарности касательного четырехугольника указаны в Касательный четырехугольник#Коллинеарные точки .
- Во вписанномчетырехугольнике центр описанной окружности , центроид вершины ( пересечение двух бимедиан) и антицентр коллинеарны. [8]
- В вписанном четырехугольнике центроид площади , центроид вершины и пересечение диагоналей лежат на одной прямой. [9]
- В касательной трапеции касания вписанной окружности с двумя основаниями коллинеарны центру вписанной окружности.
- В касательной трапеции середины катетов коллинеарны центру входящей трапеции.
Шестиугольники
- Теорема Паскаля (также известная как теорема Hexagrammum Mysticum) утверждает, что если наконическом сечении (например, эллипсе , параболе или гиперболе ) выбрать произвольные шесть точек и соединить их отрезками в любом порядке, чтобы сформировать шестиугольник , то три пары противоположных сторон шестиугольника (при необходимости удлиненных) сходятся в трех точках, лежащих на прямой линии, называемой линией Паскаля шестиугольника. Верно и обратное: теорема Брейкенриджа-Маклорена утверждает, что если три точки пересечения трех пар прямых, проходящих через противоположные стороны шестиугольника, лежат на прямой, то шесть вершин шестиугольника лежат на конике, что может быть выродиться, как в Теорема Паппа о шестиугольнике .
Конические сечения
- По теореме Монжа для любых трех окружностей на плоскости, ни одна из которых не находится полностью внутри другой, три точки пересечения трех пар прямых, каждая из которых касается двух окружностей, лежат на одной прямой.
- В эллипсе центр, два фокуса и две вершины с наименьшим радиусом кривизны коллинеарны, а центр и две вершины с наибольшим радиусом кривизны коллинеарны.
- В гиперболе центр, два фокуса и две вершины коллинеарны.
Конусы
- Центр масс конического твердого тела однородной плотности находится на четверти пути от центра основания до вершины на прямой линии, соединяющей их.
Тетраэдры
- Центроид тетраэдра – это середина между его точкой Монжа и центром описанной окружности . Эти точки определяют линию Эйлера тетраэдра, аналогичную линии Эйлера треугольника. Центр двенадцатиконечной сферы тетраэдра также лежит на линии Эйлера.
Алгебра
Коллинеарность точек, координаты которых заданы
В координатной геометрии в n -мерном пространстве набор из трех или более различных точек коллинеарен тогда и только тогда, когда матрица координат этих векторов имеет ранг 1 или меньше. Например, для трех точек X = ( x1 , x2 , . xn ) , Y = ( y1 , y2 , . , yn ) и Z = ( z1 , z2 , . , z n ), если матрица
[ Икс 1 Икс 2 … Икс н у 1 у 2 … у н г 1 г 2 … г н ] <\ displaystyle <\ begin
имеет ранг 1 или меньше, точки коллинеарны.
[ 1 Икс 1 Икс 2 … Икс н 1 у 1 у 2 … у н 1 г 1 г 2 … г н ] <\ displaystyle <\ begin
имеет ранг 2 или меньше, точки коллинеарны. В частности, для трех точек на плоскости ( n = 2) указанная выше матрица является квадратной, а точки коллинеарны тогда и только тогда, когда ее определитель равен нулю; поскольку этот определитель 3 × 3 равен удвоенной плюс или минус площади треугольника с этими тремя точками в качестве вершин, это эквивалентно утверждению, что три точки лежат на одной прямой тогда и только тогда, когда треугольник с этими точками в качестве вершин имеет нулевую площадь.
Коллинеарность точек, попарные расстояния которых заданы
Множество, состоящее как минимум из трех различных точек, называется прямым , что означает, что все точки лежат на одной прямой тогда и только тогда, когда для каждых трех из этих точек A , B и C следующий определитель определителя Кэли–Менгера равен нулю (с d ( AB ) означает расстояние между A и B и т. д .):
дет [ 0 г ( А Б ) 2 г ( А С ) 2 1 г ( А Б ) 2 0 г ( Б С ) 2 1 г ( А С ) 2 г ( Б С ) 2 0 1 1 1 1 0 ] знак равно 0. <\ displaystyle \ det <\ begin
Этот определитель по формуле Герона равен -16, умноженному на квадрат площади треугольника с длинами сторон d ( AB ), d ( BC ) и d ( AC ); поэтому проверка, равен ли этот определитель нулю, эквивалентна проверке того, имеет ли треугольник с вершинами A , B и C нулевую площадь (таким образом, вершины лежат на одной прямой).
Эквивалентно, набор из по крайней мере трех различных точек является коллинеарным тогда и только тогда, когда для каждых трех из этих точек A , B и C с d ( AC ) больше или равен каждому из d ( AB ) и d ( BC ) , неравенство треугольника d ( AC ) ≤ d ( AB ) + d ( BC ) выполняется с равенством.
Теория чисел
Два числа m и n не являются взаимно простыми , т. е. имеют общий делитель, отличный от 1, тогда и только тогда, когда для прямоугольника, построенного на квадратной решетке с вершинами в точках (0, 0), ( m , 0), ( m , n ) и (0, n ), хотя бы одна внутренняя точка коллинеарна с (0, 0) и ( m , n ).
Параллелизм (двойная плоскость)
В различных плоскостных геометриях понятие смены ролей «точек» и «линий» при сохранении отношений между ними называется плоскостной двойственностью . Учитывая набор коллинеарных точек, по двойственности плоскости мы получаем набор прямых, которые все пересекаются в общей точке. Свойство, которым обладает этот набор линий (встреча в общей точке), называется параллелизмом , а линии называются параллельными линиями . Таким образом, параллелизм — это плоское двойственное понятие по отношению к коллинеарности.
График коллинеарности
Учитывая частичную геометрию P , где две точки определяют не более одной прямой, граф коллинеарности P — это граф , вершины которого являются точками P , где две вершины смежны тогда и только тогда, когда они определяют прямую в P .
Использование в статистике и эконометрике
В статистике коллинеарность относится к линейной зависимости между двумя независимыми переменными . Две переменные являются совершенно коллинеарными , если между ними существует точная линейная зависимость, поэтому корреляция между ними равна 1 или -1. Это, Икс 1 <\ Displaystyle X_ <1>> 



Икс 2 я знак равно λ 0 + λ 1 Икс 1 я . <\ displaystyle X_ <2i>= \ lambda _ <0>+ \ lambda _ <1>X_ <1i>.>
Это означает, что если различные наблюдения ( X 1 i , X 2 i ) нанесены на плоскость ( X 1 , X 2 ), эти точки будут коллинеарны в смысле, определенном ранее в этой статье.
Совершенная мультиколлинеарность относится к ситуации, в которой k ( k ≥ 2) независимых переменных в модели множественной регрессии совершенно линейно связаны, согласно
Икс к я знак равно λ 0 + λ 1 Икс 1 я + λ 2 Икс 2 я + ⋯ + λ к − 1 Икс ( к − 1 ) , я <\ displaystyle X_
для всех наблюдений i . На практике мы редко сталкиваемся с идеальной мультиколлинеарностью в наборе данных. Чаще проблема мультиколлинеарности возникает, когда существует «сильная линейная связь» между двумя или более независимыми переменными, что означает, что
Икс к я знак равно λ 0 + λ 1 Икс 1 я + λ 2 Икс 2 я + ⋯ + λ к − 1 Икс ( к − 1 ) , я + ε я <\ displaystyle X_
Концепция латеральной коллинеарности расширяет эту традиционную точку зрения и относится к коллинеарности между объяснительными и критериальными (т.е. объясняемыми) переменными. [10]
Использование в других областях
Антенные решетки
В телекоммуникациях коллинеарная ( или коллинеарная) антенная решетка представляет собой решетку дипольных антенн , установленных таким образом, что соответствующие элементы каждой антенны параллельны и соосны, то есть расположены вдоль общей линии или оси.
Фотография
Уравнения коллинеарности представляют собой набор из двух уравнений, используемых в фотограмметрии и компьютерном стереозрении для связи координат в плоскости изображения ( сенсора ) (в двух измерениях) с координатами объекта (в трех измерениях). В условиях фотографии уравнения выводятся с учетом центральной проекции точки объекта через оптический центр камеры. к изображению в плоскости изображения (сенсора). Три точки, точка объекта, точка изображения и оптический центр, всегда коллинеарны. Другой способ сказать это состоит в том, что все отрезки линии, соединяющие точки объекта с точками их изображения, совпадают в оптическом центре. [11]
Источник статьи: http://wikipredia.net/ru/Collinearity
Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R
Координатная форма условия коллинеарности векторов
Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .
По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ – произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Исходные данные: векторы a → = ( 3 – 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 – 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 – 2 2 ) = 1 3 2 – 4 + 3 – 2 2 = 1 2 – 1 b y = λ · a y ⇔ 2 + 1 = 1 2 – 1 · 1 ⇔ ( 2 + 1 ) · ( 2 – 1 ) = 1 ⇔ 1 ≡ 1
Т.е. b → = 1 2 – 1 · a → , следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 1 , 0 , – 2 ) и b → = ( – 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.
Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ – 3 = – 3 · 1 0 = – 3 · 0 6 = – 3 · ( – 2 ) , то верным будет равенство: b → = – 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 – 2 – 3 0 6 = i → · 0 · 6 + j → · ( – 2 ) · ( – 3 ) + k → · 1 · 0 – k → · 0 · ( – 3 ) – j → · 1 · 6 – i → · ( – 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Исходные данные: вектор a → = ( 2 , – 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Ответом может послужить, например, 1 2 · a → = ( 1 , – 3 ) или вектор 3 · a → = ( 6 , – 18 ) .
Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , – 3 ) .
Исходные данные: вектор a → = ( 3 , 4 , – 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( – 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , – 1 2 )
Источник статьи: http://zaochnik.com/spravochnik/matematika/vektory/uslovie-kollinearnosti-vektorov/
Коллинеарные векторы – условия, признаки и примеры
Общие сведения
Вектором называют направленный отрезок, который имеет начало и конец. Обозначают его либо большими буквами, либо маленькими, например, АБ или a. Над буквой ставится знак вектора — стрелка. Любой отрезок характеризуется длиной, которую называют модулем. Если начало и конец прямой совпадают, то такой вектор носит название нулевой и обозначается в виде точки. При этом его модуль будет равняться нулю.
Для равенства векторов необходимо выполнение двух условий:
- модули отрезков должны быть равны;
- сравниваемые отрезки должны быть направлены в одну сторону.
Равные вектора могут быть совмещены параллельным переносом, при этом начало и конец отрезков должны совпадать. Если ограниченные линии не являются равными, но лежат на параллельных прямых, то их называют коллинеарными, то есть, по определению коллинеарных векторов, их направление для определения признака не является важным.
Коллинеарность является одним из признаков сонаправленности, но для выполнения последнего они должны ещё и совпадать по направлению. Наглядным понятием, объясняющим сонаправленность, является прямое движение транспорта или пешехода. Например, если рассматривать две траектории движения как векторы АБ и СД, лежащие на плоскости, при этом их лучи лежат в одной полуплоскости и перпендикулярны её границам, то их можно назвать сонаправленными.
Поэтому параллельные отрезки будут направлены в одну сторону лишь тогда, когда их лучи находятся по одну сторону от прямой, соединяющей их начала. При этом если векторы коллинеарны, но не сонаправлены, то они будут являться противоположными.
С векторами можно выполнять любые простейшие арифметические операции. При сложении используют правила параллелограмма и треугольника. Пусть есть два отрезка, имеющие общее начало. Для того чтобы найти их сумму, необходимо фигуру достроить до параллелограмма. Диагональ этой фигуры и будет искомой величиной. Когда же конец одного отрезка является началом другого, то, соединив свободные точки, можно получить треугольник. Новая прямая и будет являться вектором суммы. Следует отметить, что эти правила равнозначны друг другу. Вычитание отрезков находится аналогично.
Вектор можно и умножить на число, то есть длина отрезка увеличивается на значение множителя. Если в произведении стоит отрицательное число, то характеристика меняет направление.
Критерии коллинеарности
Теорема критерия коллинеарности представляет собой утверждение, которое сообщает, что если есть два не ортогональных отрезка, одинаковых по длине, a и b, то вектор a может быть выражен через формулу a || b = a = y * b. При этом y обозначает любое произвольное число. Есть и обратное утверждение: если вектор b умножить на число и получится отрезок a, то тогда a и b будут коллинеарными.
Эти два правила тождественны и называются критериями коллинеарности. Для их доказательства нужно знать правило арифметических действий с параллельными и перпендикулярными векторами, а также понимать основной базис. Заключается он в том, что если имеются три отрезка a, b и c, при этом верной является следующая комбинация a || b и a || c, то справедливо утверждать, что b || c.
Для того чтобы доказать свойство a || b = a = y * b, нужно воспользоваться определением коллинеарности. Из него следует, что если a || b, то отрезки могут быть сонаправлены или противоположно направлены. Таким образом, необходимо проверить утверждение для двух случаев:
Если предположения окажутся верными, то можно будет сделать вывод о справедливости записи для других случаев. То есть к любым параллельным отрезкам можно применить равенство a = u * b. Этот критерий занимает важное место в геометрии наряду со свойствами перпендикулярности (ортогональности) прямых.
Сонаправленные вектора
Пусть a и b однонаправленные. Введём число y, равное отношению a на b. Так как длина вектора может быть только положительной, то и y = a /b > 0. Состояние вектора, когда он нулевой, является частным случаем и его можно не рассматривать, так как при этом получится равенство 0 = 0. Если длину b умножить на число, то получится новый вектор. Пусть это будет отрезок c, то есть с = y * b. Учитывая свойство коллинеарности, можно утверждать, что между c и b останется параллельность.
По условию известно, что a || b. Исходя из транзитивности отрезков, можно заключить, что и c || b. Теперь необходимо установить их направление. Изначально a и b направлены в одну сторону. Ведённый множитель больше нуля. Это значит, что после умножения направление вектора не изменится, то есть c будет иметь то же направление что и b. Тогда получается, что a || b и c || b. Отсюда следует, что a || с.
Длина вектора c равняется |c| = |u| * |b|. Вместо u можно подставить a / b. В итоге получится |a| * |b| / |b| = |a|. Таким образом, два условия выполняются, и можно утверждать, что с = a. Получается, что для двух любых однонаправленных векторов будет выполняться правило a = u * b.
Противоположные отрезки
Пусть имеется два отрезка a и b, при этом их направления противоположны друг другу. Можно ввести переменную u, которая будет меньше нуля. Тогда справедливо записать u = – |a| / |b| 0, так как |m| ↑↑ |n|. Отсюда u = 240 / 12 = 20.
Использование онлайн-калькулятора
Решение простых заданий из школьного курса обычно не вызывает сложностей. Но на практике приходится сталкиваться со сложными выражениями. Для их вычисления нужно проявить усидчивость и при этом быть предельно внимательным. Кроме этого, расчёт занимает довольно много времени, а любая, казалось бы, незначительная оплошность, приведёт к неправильному решению.
Поэтому условие коллинеарности векторов удобно проверять на так называемых онлайн-калькуляторах. Это обычно мощные сервисы, основная деятельность которых заключается в предоставлении услуг по автоматизации вычислений. Среди них попадаются и сайты, умеющие вычислять и вектора.
Для того чтобы выполнить на них математические операции, необходимо иметь доступ к интернету и установленный веб-обозреватель. Всё, что требуется от пользователя, это просто зайти на сайт и выбрать раздел, связанный с операциями над векторами. Затем в предложенную форму вести условие задания и запустить расчёт нажатием одной кнопки.
Из множества онлайн-расчётчиков, доступных в секторе рунета, можно выделить следующие:
- SolverBook — это простой на вид сайт, содержащий на своей странице приложение, позволяющее выполнять любые действия над отрезками, а также определять их вид. Кроме непосредственного предоставления ответа, сервис выдаёт пошаговое решение. При этом каждый этап будет детально расписан.
- O nlineMSchool — сайт помогает найти коллинеарные отрезки для любой сложности примеров. На страницах сервиса находится вся необходимая теория и примеры решения заданий. Поэтому даже слабо подготовленный пользователь сможет разобраться во всех нюансах решения нужных ему задач.
- Kontrolnaya-rabota — отличительной его чертой является возможность отправления подробного решения на указанную электронную почту. Сайт умеет работать как с парой векторов, так и попарной системой.
Все указанные сервисы предоставляют доступ к услугам бесплатно и без регистрации. Воспользовавшись онлайн-калькуляторами, даже слабо подготовленный пользователь научится самостоятельно определять коллинеарность. Такие расчётчики будут полезны и учащимся, и инженерам.
Источник статьи: http://nauka.club/matematika/kollinearny%D0%B5-vektor%D1%83.html
Геометрия
Понятие вектора в пространстве
Напомним, что в курсе планиметрии мы уже подробно изучали вектора и действия с ними. При этом предполагалось, что все вектора располагаются в одной плоскости. Однако можно расширить понятие вектора так, чтобы они использовались и в стереометрии. В таком случае вектора уже могут располагаться в различных плоскостях.
Начнем с определения вектора:
Конец вектора обозначают с помощью стрелки. Посмотрим на рисунок:
Здесь показаны сразу три вектора:
У вектора АВ начало находится в точке А, а конец – в точке В. Аналогично у вектора С D точка С – это начало, а D – это конец. В обоих случаях начало и конец – это различные точки, поэтому АВ и CD именуют ненулевыми векторами. Если же начало и конец находятся в одной точке, например в Т, то получается нулевой вектор ТТ. Всякую точку в пространстве можно рассматривать как нулевой вектор:
Длина вектора АВ – это длина соответствующего ему отрезка АВ. Для обозначения длины используют квадратные скобки:
Естественно, что нулевой вектор имеет нулевую длину.
Далее напомним понятие коллинеарных векторов:
Коллинеарные вектора могут быть либо сонаправленными, либо противоположно направленными. Сонаправленные вектора находятся на сонаправленных лучах. Рассмотрим пример с кубом:
Здесь показаны вектора AD и ВС. Они сонаправленные, этот факт записывается так:
Вектора AD и FE располагаются на скрещивающихся прямых, поэтому они не коллинеарны. Их нельзя считать ни сонаправленными, ни противоположно направленными.
Сонаправленные вектора, имеющие одинаковую длину, именуются равными.
Рассмотрим несколько простейших задач.
Задание. В прямоугольном параллелепипеде АВС DA 1 B 1 C 1 D 1 известны три его измерения:
Решение. Для нахождения длин этих векторов достаточно вычислить длину отрезков СВ, DB и DB 1. Проще всего вычислить СВ, ведь отрезки СВ и AD одинаковы как стороны прямоугольника АВ CD :
Задание. На рисунке показан правильный тетраэдр АВС D . Точки M , N , P и Q являются серединами тех сторон, на которых они располагаются. Какие вектора из отмеченных на рисунке равны между собой?
Решение. Легко заметить, что вектора DP и PC находятся на одной прямой DC и сонаправлены, при этом их длина одинакова, ведь Р – середина DC . Тогда эти вектора по определению равны:
Вектора АМ и МВ также коллинеарны и имеют одинаковую длину, но они противоположно направлены, а потому равными не являются.
Теперь заметим, что отрезки MN , MQ , PQ и NP – это средние линии в ∆ ABD , ∆ АВС, ∆ BCD и ∆ ACD соответственно. По свойству средней линии получаем, что MN || BD , PQ || BD , MQ ||АС и NP ||АС. Отсюда по свойству транзитивности параллельности получаем, что MN || PQ и MQ || NP . Это значит, что четырехугольник MQPN – это параллелограмм, а у него противоположные стороны одинаковы:
Операции над векторами
Правила сложения векторов в стереометрии не отличаются от правил в планиметрии. Пусть надо сложить два вектора, а и b . Для этого отложим вектор а от какой-нибудь точки А, тогда его конец окажется в некоторой точке В. Далее от В отложим вектор b , его конец попадет в какую-то точку С. Тогда вектор АС как раз и будет суммой a и b :
Такой метод сложения векторов именуется правилом треугольника. Если нужно сложить больше двух векторов, то используют правило многоугольника. В этом случае необходимо каждый следующий вектор откладывать от конца предыдущего. При этом в стереометрии вектора могут располагаться в различных плоскостях, то есть они на самом деле многоугольник не образуют:
Напомним, что в планиметрии существовали так называемые противоположные вектора. Есть они и в стереометрии:
Главное свойство противоположных векторов заключается в том, что в сумме они дают нулевой вектор:
Заметим, что для получения противоположного вектора достаточно поменять его начало и конец, то есть в записи вектора обозначающие его буквы надо просто записать в обратном порядке:
C помощью противоположного вектора легко определить операцию вычитания векторов. Чтобы из вектора а вычесть вектор b , надо всего лишь прибавить к a вектор, противоположный b :
Далее рассмотрим умножение вектора на число. Пусть вектор а умножается на число k . В результате получается новый вектор b , причем
1) b и a будут коллинеарными векторами;
2) b будет в k раз длиннее, чем вектор a .
Если k – положительное число, то вектора a и b будут сонаправленными. Если же k a и b будут направлены противоположно.
Уточним, что если | k | b будет не длиннее, а короче вектора a . Наконец, если k = 0, то и b будет иметь нулевую длину, то есть b окажется нулевым вектором.
Задание. Дан параллелепипед АВС D А1В1С1 D 1. Постройте вектор, который будет являться суммой векторов:
Решение. В каждом случае необходимо заменить один из векторов в сумме на другой равный ему вектор так, чтобы можно было применить правило треугольника.
В задании а) вектор А1 D 1 заменить равным ему вектором ВС. В итоге получится вектор АС.
В задании б) заменяем А D 1 на вектор ВС1. Также можно было бы заменить АВ на D 1 C 1. В обоих случаях сумма окажется равной АС1.
В задании в) удобно DA заменить на C 1В1, тогда искомой суммой будет вектор С1В.
В задании г) производим замену DD 1 на равный ему вектор BB 1. Тогда сумма DB и BB 1– это вектор DB 1.
В задании д) необходимо заменить ВС на В1С1. В итоге получаем вектор DC :
Задание. В пространстве отмечены точки А, В, С и D . Выразите вектор АВ через вектора:
Решение. В случае а) сначала запишем очевидное равенство векторов, вытекающее из правило многоугольника:
Обратите внимание, что здесь у каждого следующего слагаемого начальная точка совпадает с конечной точкой предыдущего слагаемого, поэтому равенство и справедливо:
Однако по условию а) нам надо использовать другие вектора для выражения АВ. Мы можем просто заменить вектора CD и DB на противоположные:
Теперь можно составить и выражение для АВ:
Аналогично решаем и задания б) и в):
Задание. Р – вершина правильной шестиугольной пирамиды. Докажите, что сумма векторов, совпадающих с ребрами этой пирамиды и начинающихся в точке Р, в точности равна сумме векторов, которые совпадают с апофемами пирамиды и при этом также начинаются в точке Р.
Решение. Обозначим вершины буквами А1, А2, … А6, а середины сторон шестиугольника, лежащего в основании, буквами Н1, Н2, … Н6, как это показано на рисунке:
Нам надо показать, что сумма красных векторов равна сумме черных векторов:
Теперь отдельно построим правильный шестиугольник, лежащий, в основании пирамиды:
Ясно, что вектора, образованные сторонами этого шестиугольника, в сумме дают нулевой вектор (по правилу многоугольника):
Так как точки Н1, Н2, … Н6 – середины сторона, то вектора Н6А6, Н5А5,…Н1А1 будут вдвое короче векторов А1А6, А6А5, … А2А1. При этом они находятся на одних прямых, поэтому справедливы равенства:
Таким образом нам удалось из верного равенства (3) доказать (2), из которого в свою очередь следует справедливость и (1), ч. т. д.
Задание. Упростите выражения:
Решение. Здесь надо просто применить законы сложения и умножения векторов, как это делалось и в курсе планиметрии. Сначала раскрываем скобки, а потом приводим подобные слагаемые:
Компланарные векторы
Если мы отложим несколько векторов от одной точки, то они либо будут находиться в одной плос-ти, либо располагаться в различных плос-тях. В первом случае их именуют компланарными векторами, а во втором – некомпланарными.
Любые два вектора будут компланарны, ведь при их откладывании от одной точки мы получаем две пересекающихся прямых, а через них всегда можно провести плос-ть. Однако если векторов более двух, то они могут быть как компланарны, так и некомпланарны.
Рассмотрим для примера параллелепипед:
Здесь вектора АС, АВ и АD компланарны, так как все они принадлежат одной грани (то есть плос-ти) АВСD. А вектора АВ, АD и АА1 некомпланарны, ведь через них нельзя провести одну плос-ть.
Очевидно, что если из трех векторов любые два коллинеарны, то вся тройка векторов компланарна, ведь при откладывании векторов от одной точки коллинеарные вектора окажутся на одной прямой.
Существует признак компланарности векторов:
Напомним, что подразумевается под разложением вектора. Пусть есть вектора а, b и c. Если существуют такие числах и y, при которых выполняется равенство
то говорят, что вектор с разложен по векторам а и b, причем числа xи y называются коэффициентами разложения.
Докажем сформулированный признак. Пусть есть три вектора а, b и c, а также числа xи y, такие, что
Эти вектора находятся в одной плос-ти ОАВ. Теперь от той же точки О отложим вектора ха и уb, концы которых окажутся в точках А1 и В1:
Естественно, что вектора ОА1 и ОВ1 также окажутся в плос-ти ОАВ. Тогда и их сумма будет принадлежать этой плос-ти, а эта сумма как раз и есть вектор с:
В итоге получили, что а, b и с располагаются в одной плос-ти, то есть они компланарны.
Справедливо и обратное утверждение. Если вектора а, b и с компланарны, но а и b неколлинеарны, то вектор с можно разложить на вектора a и b. Это утверждение прямо следует из изученной в 9 классе теоремы о разложении векторов. Важно отметить, что коэффициенты такого разложения определяются однозначно.
Для сложения тройки некомпланарных векторов можно применить так называемое правило параллелепипеда. Если есть три некомпланарных вектора, то можно отложить их от одной точки О и далее построить параллелепипед, в котором эти вектора будут ребрами. Тогда диагональ этого параллелепипеда, выходящая из точки О, и будет суммой этих трех векторов:
Разложение вектора на некомпланарные вектора
Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:
Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:
Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р1. (Примечание. Если Р принадлежит α, то точки Р и Р1 совпадут, то есть вектор Р1Р будет нулевым).
Далее через точку Р1 в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р2. Заметим, что вектор ОР2 находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что
Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х1, у1 и z1:
В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:
Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.
Задание. АВСD и А1В1С1D1 – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ1, СС1 и DD1 компланарна.
Решение. Сначала построим рисунок по условию задачи:
Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.
В результате нам удалось разложить СС1 на вектора BB1 и CC1. Значит, эти три вектора коллинеарны.
Задание. В параллелепипеде АВСDA1B1C1D1 запишите разложение вектора BD1 по векторам ВА, ВС и ВВ1.
Решение. Сначала представим вектор BD1 как сумму трех векторов:
Теперь заметим, что вектора С1D1 и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС1 и ВВ1:
Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.
Решение. Сначала запишем очевидное выражение для вектора DK:
Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.
Решение. Медиану, проходящую через точку А, мы обозначим как АА1, то есть А1 – это середина отрезка ВС. Также буквой К обозначим середину ОВ:
Сначала разложим вектор ОА1 на ОВ и ОС. Это можно сделать, ведь они компланарны. КА1 – это средняя линия ∆ОСВ, поэтому КА1||ОС и КА1 вдвое короче ОС. Это значит, что
Так как АА1 – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:
Только что решенная задача может быть использована и при решении другого, более сложного задания.
Задание. Докажите, что в параллелепипеде АВСDА1В1С1D1 плос-ти А1ВD и СB1D1 делят диагональ АС1 на три равных отрезка.
Решение. Обозначим точкой K точку пересечения медиан ∆А1ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что
Это соотношение означает, что вектора АК и АС1 коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС1, и отрезок АК втрое короче диагонали.
Аналогично можно показать, что и
Из этого также вытекает, что М принадлежит диагонали АС1, и МС1 втрое короче АС1. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.
Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.
Источник статьи: http://100urokov.ru/predmety/vektora-v-prostranstve
Коллинеарность – Collinearity
| Найти коллинеарность или коллинеарность в Викисловаре, бесплатный словарь. |
В геометрии, коллинеарность набора точек – это свойство их расположения на единственной строке. Набор точек с этим свойством называется коллинеарным (иногда обозначается как коллинеарным ). В более общем смысле этот термин использовался для выровненных объектов, то есть вещей, находящихся «в линию» или «в ряд».
Содержание
- 1 Точки на прямой
- 2 Примеры евклидовой геометрии
- 2.1 Треугольники
- 2.2 Четырехугольники
- 2.3 Шестиугольники
- 2.4 Конические сечения
- 2.5 Конусы
- 2.6 Тетраэдры
- 3 Алгебра
- 3.1 Коллинеарность точек с заданными координатами
- 3.2 Коллинеарность точек с заданными попарными расстояниями
- 4 Теория чисел
- 5 Параллелизм (двойная плоскость)
- 6 График коллинеарности
- 7 Использование в статистике и эконометрике
- 8 Использование в других областях
- 8.1 Антенные решетки
- 8.2 Фотография
- 9 См. Также
- 10 Примечания
- 11 Ссылки
Точки на line
В любой геометрии набор точек на линии называется коллинеарным . В евклидовой геометрии это соотношение интуитивно визуализируется точками, лежащими в ряд на «прямой линии». Однако в большинстве геометрий (включая евклидову) линия обычно является примитивным (неопределенным) типом объекта, поэтому такие визуализации не обязательно подходят. Модель для геометрии предлагает интерпретацию того, как точки, линии и другие типы объектов связаны друг с другом, и такое понятие, как коллинеарность, должно интерпретироваться в контексте этой модели. Например, в сферической геометрии, где линии представлены в стандартной модели большими окружностями сферы, наборы коллинеарных точек лежат на одной большой окружности. Такие точки не лежат на «прямой линии» в евклидовом смысле и не считаются расположенными в ряд.
Отображение геометрии на себя, при котором линии переходят в линии, называется коллинеацией ; он сохраняет свойство коллинеарности. линейные карты (или линейные функции) из векторных пространств, рассматриваемые как геометрические карты, отображают линии в линии; то есть они сопоставляют наборы коллинеарных точек с наборами коллинеарных точек и, таким образом, являются коллинеациями. В проективной геометрии эти линейные отображения называются гомографиями и представляют собой всего лишь один тип коллинеации.
Примеры в евклидовой геометрии
Треугольники
В любом треугольнике следующие наборы точек коллинеарны:
- ортоцентр, центр окружности, центроид , точка Эксетера, точка де Лоншампа и центр окружности из девяти точек коллинеарны, все они попадают на линию, называемую линией Эйлера.
- Точка де Лоншампа также имеет другие коллинеарности.
- Любая вершина, касание противоположной стороны с вневписанной окружностью, и точка Нагеля коллинеарны в линии, называемой разделителем треугольника.
- Середина любой стороны, точка, которая равноудалена от нее вдоль граница треугольника в любом направлении (таким образом, эти две точки делят периметр пополам), а центр круга Шпикера коллинеарны на линии, называемой разделителем треугольник. (Круг Шпикера – это вписанная окружностьсреднего треугольника, а его центр – это центр масспериметра треугольника.)
- Любая вершина, касание противоположной стороны с вписанной окружностью и точка Жергонна коллинеарны.
- Из любой точки описанной окружности треугольника ближайшие точки на каждой из трех вытянутых сторон треугольника коллинеарны на линии Симсона точки на описанной окружности.
- Линии, соединяющие основания высот, пересекают противоположные стороны в коллинеарных точках.
- Центр треугольника , средняя точка высота, и точка контакта соответствующей стороны с вневписанной окружностью относительно этой стороны коллинеарны.
- Теорема Менелая утверждает, что три точки P 1, P 2, P 3 <\ displaystyle P_ <1>, P_ <2>, P_ <3>>
на сторонах (некоторые расширенные ) противоположного треугольника вершины сайта A 1, A 2, A 3 <\ displaystyle A_ <1>, A_ <2>, A_ <3>>
соответственно коллинеарны тогда и только тогда, когда следующие произведения длин сегментов равны:
P 1 A 2 ⋅ P 2 A 3 ⋅ P 3 A 1 = P 1 A 3 ⋅ P 2 A 1 ⋅ P 3 A 2. <\ Displaystyle P_ <1>A_ <2>\ cdot P_ <2>A_ <3>\ cdot P_ <3>A_ <1>= P_ <1>A_ <3>\ cdot P_ <2>A_ <1>\ cdot P_ <3>A_ <2>.>
- Центр тяжести, центроид и центр круга Шпикера лежат на одной прямой.
- Центр описанной окружности, средняя точка Брокара и Точка лемуана треугольника коллинеарна.
- Две перпендикулярные прямые, пересекающиеся в ортоцентре треугольника, каждая пересекает каждую из точек расширенные стороны. Середины на трех сторонах этих точек пересечения коллинеарны в прямой Дроза – Фарни.
Четырехугольники
- В выпуклом четырехугольнике ABCD, противоположные стороны которого пересекаются в точках E и F, средние точки AC, BD и EF коллинеарны, и линия, проходящая через них, называется линией Ньютона (иногда известной как линия Ньютона-Гаусса ). Если четырехугольник является касательным четырехугольником, то его центр также лежит на этой прямой.
- В выпуклом четырехугольнике квазиортоцентр H, «центр тяжести площади» G и квазицикругцентр O являются коллинеарны в этом порядке, и HG = 2GO. (См. Четырехугольник # Замечательные точки и линии в выпуклом четырехугольнике.)
- Другие коллинеарности тангенциального четырехугольника приведены в Тангенциальном четырехугольнике # Коллинеарные точки.
- В циклическом четырехугольник, центр описанной окружности, центроид вершины (пересечение двух бимедианов) и антицентр лежат на одной прямой.
- В циклическом четырехугольнике центр тяжести площади , центр тяжести вершины и пересечение диагоналей коллинеарны.
- В тангенциальной трапеции касания вписанная окружность с двумя основаниями коллинеарна центру.
- В тангенциальной трапеции средние точки ног коллинеарны центру.
Шестиугольники
- Теорема Паскаля (также известная как теорема Hexagrammum Mysticum) утверждает, что если выбраны произвольные шесть точек на коническом сечении (т. е. эллипсе, параболе или гипербола ), к которой присоединяется l Если сегменты расположены в любом порядке, образуя шестиугольник, то три пары противоположных сторон шестиугольника (при необходимости удлиненные) встречаются в трех точках, которые лежат на прямой линии, называемой линией Паскаля шестиугольника. Верно и обратное: теорема Брейкенриджа – Маклорена утверждает, что если три точки пересечения трех пар прямых, проходящих через противоположные стороны шестиугольника, лежат на одной прямой, то шесть вершин шестиугольника лежат на одной прямой. коника, которая может быть вырожденной, как в теореме Паппа о шестиугольнике.
Конические сечения
- По теореме Монжа, для любых трех окружностей на плоскости, ни одна из которых полностью внутри одной из других, три точки пересечения трех пар прямых, каждая из которых касается двух окружностей, коллинеарны.
- В эллипсе центр, два фокуса и две вершины с наименьшим радиусом кривизны коллинеарны, а центр и две вершины с наибольшим радиусом кривизны коллинеарны.
- В гиперболе центр, два фокуса и две вершины коллинеарны.
Конусы
Тетраэдры
Алгебра
Коллинеарность точек, координаты которых заданы
В координате geometry, в n-мерном пространстве набор из трех или более различных точек коллинеарен тогда и только тогда, когда матрица координат этих векторов имеет rank 1 или меньше. Например, для трех точек X = (x 1, x 2. x n), Y = (y 1, y 2. y n) и Z = (z 1, z 2. z n), если матрица
[x 1 x 2… xny 1 y 2… ynz 1 z 2… zn] <\ displaystyle <\ begin
имеет ранг 1 или меньше, точки коллинеарны.
Эквивалентно для каждого подмножества из трех точек X = (x 1, x 2. x n), Y = (y 1, y 2. y n) и Z = (z 1, z 2. z n), если матрица
[1 x 1 x 2… xn 1 y 1 y 2… yn 1 z 1 z 2… zn] <\ displaystyle <\ begin
имеет rank 2 или меньше, точки лежат на одной прямой. В частности, для трех точек на плоскости (n = 2) указанная выше матрица является квадратной, а точки коллинеарны тогда и только тогда, когда ее определитель равен нулю; поскольку этот определитель 3 × 3 в два раза больше или меньше площади треугольника с этими тремя точками в качестве вершин, это эквивалентно утверждению, что три точки коллинеарны тогда и только тогда, когда треугольник с этими точками поскольку вершины имеют нулевую площадь.
Коллинеарность точек, попарные расстояния которых заданы
Набор по крайней мере из трех различных точек называется прямыми, что означает, что все точки коллинеарны, если и только если, для каждых трех из этих точек A, B и C следующий определитель определителя Кэли-Менгера равен нулю (где d (AB) означает расстояние между A и B и т. д.):
det [0 d (AB) 2 d (AC) 2 1 d (AB) 2 0 d (BC) 2 1 d (AC) 2 d (BC) 2 0 1 1 1 1 0] = 0. <\ displaystyle \ det <\ begin
Этот определитель, согласно формуле Герона, равен −16 квадрату площади треугольника со сторонами d (AB), d (BC) и d (AC); поэтому проверка того, равен ли этот определитель нулю, эквивалентна проверке, имеет ли треугольник с вершинами A, B и C нулевую площадь (так что вершины коллинеарны).
Эквивалентно, набор, по крайней мере, из трех различных точек коллинеарен тогда и только тогда, когда для каждых трех из этих точек A, B и C с d (AC) больше или равно каждой из d (AB) и d (BC), неравенство треугольника d (AC) ≤ d (AB) + d (BC) выполняется с равенством.
Теория чисел
Два числа m и n не являются взаимно простыми – то есть у них есть общий множитель, отличный от 1, – тогда и только тогда, когда для прямоугольника, нанесенного на квадратная решетка с вершинами в (0, 0), (m, 0), (m, n) и (0, n), по крайней мере одна внутренняя точка коллинеарна с (0, 0) и (m, n).
Параллелизм (двойная плоскость)
В различных плоских геометриях понятие смены ролей «точек» и «линий» при сохранении взаимосвязи между ними называется плоская двойственность. Учитывая набор коллинеарных точек, по двойственности плоскости мы получаем набор прямых, все из которых пересекаются в общей точке. Свойство, которым обладает этот набор строк (встреча в общей точке), называется параллелизм, а строки называются параллельными строками. Таким образом, параллелизм – это плоское понятие, двойственное коллинеарности.
График коллинеарности
Учитывая частичную геометрию P, где две точки определяют не более одной линии, график коллинеарности P равен граф, вершинами которого являются точки P, где две вершины смежны с тогда и только тогда, когда они определяют линию в P.
Использование в статистике и эконометрике
В статистике, коллинеарность относится к линейной зависимости между двумя независимыми переменными. Две переменные идеально коллинеарны, если между ними существует точная линейная связь, поэтому корреляция между ними равна 1 или -1. То есть X 1 <\ displaystyle X_ <1>> 



X 2 i = λ 0 + λ 1 X 1 i. <\ displaystyle X_ <2i>= \ lambda _ <0>+ \ lambda _ <1>X_ <1i>.>
Это означает, что если различные наблюдения (X 1i, X 2i) нанесены на плоскость (X 1, X 2), эти точки коллинеарны в смысле, определенном ранее в этой статье.
Совершенная мультиколлинеарность относится к ситуации, в которой k (k ≥ 2) независимых переменных в модели множественной регрессии совершенно линейно связаны, согласно
X ки знак равно λ 0 + λ 1 Икс 1 я + λ 2 Икс 2 я + ⋯ + λ К – 1 Икс (к – 1), я <\ displaystyle X_
для всех наблюдений i. На практике мы редко сталкиваемся с идеальной мультиколлинеарностью в наборе данных. Чаще проблема мультиколлинеарности возникает, когда существует «сильная линейная связь» между двумя или более независимыми переменными, что означает, что
X ki = λ 0 + λ 1 X 1 i + λ 2 X 2 i + ⋯ + λ к – 1 Икс (к – 1), я + ε я <\ Displaystyle X_
где дисперсия ε i <\ displaystyle \ varepsilon _ > 
Концепция боковой коллинеарности расширяет эту традиционную точку зрения и относится к коллинеарности между объясняющими и критериями (т. Е. Объясненными) переменными.
Использование в других областях
Антенные массивы
В телекоммуникациях коллинеарная (или коллинеарная) антенная решетка представляет собой решетку из дипольные антенны установлены таким образом, что соответствующие элементы каждой антенны параллельны и выровнены, то есть они расположены вдоль общей линии или оси.
Фотография
Уравнения коллинеарности – это набор из двух уравнений, используемых в фотограмметрии и дистанционном зондировании для связи координаты в плоскости изображения (датчик ) (в двух измерениях) с координатами объекта (в трех измерениях). В параметрах фотографии уравнения выводятся путем рассмотрения центральной проекции точки объекта через оптический центр камеры на изображение в плоскость изображения (сенсора). Три точки, точка объекта, точка изображения и оптический центр, всегда коллинеарны. Другой способ сказать это: все отрезки линии, соединяющие точки объекта с точками их изображения, совпадают в оптическом центре.
Источник статьи: http://ru.wikibrief.org/wiki/Collinearity
Коллинеарная система и примеры
коллинеарные векторы Они являются одним из трех типов существующих векторов. Речь идет о тех векторах, которые находятся в одном направлении или направлении действия. Это означает следующее: два или более векторов будут коллинеарными, если они расположены в виде прямых линий, параллельных друг другу.
Вектор определяется как величина, применяемая к телу, и характеризуется как имеющий направление, смысл и масштаб. Векторы могут быть найдены в плоскости или в пространстве и могут быть разных типов: коллинеарные векторы, параллельные векторы и параллельные векторы.
- 1 колинеальный вектор
- 2 Характеристики
- 2.1 Пример 1
- 2.2 Пример 2
- 2.3 Пример 1
- 3 Коллинеарная векторная система
- 3.1 Коллинеарные векторы с противоположными значениями
- 3.2 Коллинеарные векторы с одинаковым смыслом
- 3.3 Коллинеарные векторы с равными величинами и противоположными значениями
- 4 Разница между коллинеарными и параллельными векторами
- 5 ссылок
Коллинеарные векторы
Векторы коллинеарны, если линия действия одного является точно такой же линией действия всех других векторов, независимо от размера и смысла каждого из векторов..
Векторы используются в качестве представлений в различных областях, таких как математика, физика, алгебра, а также в геометрии, где векторы коллинеарны только тогда, когда их направление одинаково, независимо от того, имеет ли их значение значение.
черты
– Два или более вектора коллинеарны, если соотношение между координатами равно.
Пример 1
У нас есть векторы m = m_x; m_y и n = n_x; n_y. Они коллинеарны, если:
Пример 2
– Два или более векторов коллинеарны, если произведение или вектор умножения равен нулю (0). Это связано с тем, что в системе координат каждый вектор характеризуется своими соответствующими координатами, и если они пропорциональны друг другу, векторы будут коллинеарными. Это выражается следующим образом:
Пример 1
У нас есть векторы a = (10, 5) и b = (6, 3). Чтобы определить, являются ли они коллинеарными, применяется теория детерминантов, которая устанавливает равенство перекрестных произведений. Таким образом, вы должны:
Коллинеарная векторная система
Коллинеарные векторы представлены графически с использованием направления и смысла их, учитывая, что они должны проходить через точку приложения и модуль, который имеет определенный масштаб или длину.
Система коллинеарных векторов формируется, когда два или более векторов воздействуют на объект или тело, представляя силу и действуя в одном направлении..
Например, если к телу приложены две коллинеарные силы, их результат будет зависеть только от направления, в котором они действуют. Есть три случая, которые:
Коллинеарные векторы с противоположными чувствами
Результирующий из двух коллинеарных векторов равен сумме этих:
пример
Если на тележку F действуют две силы1 = 40 Н и F2 = 20 Н в обратном направлении (как показано на рисунке), результат:
Коллинеарные векторы с одинаковым смыслом
Величина результирующей силы будет равна сумме коллинеарных векторов:
пример
Если на тележку F действуют две силы1 = 35 Н и F2 = 55 Н в том же направлении (как показано на рисунке), результат:
Положительный результат показывает, что коллинеарные векторы действуют влево.
Коллинеарные векторы с одинаковыми величинами и противоположными значениями
Результирующий из двух коллинеарных векторов будет равен сумме коллинеарных векторов:
Поскольку силы имеют одинаковую величину, но в противоположном направлении, то есть одно будет положительным, а другое отрицательным, при сложении двух сил результирующее значение будет равно нулю.
пример
Если на тележку F действуют две силы1 = -7 N и F2 = 7 Н, которые имеют ту же величину, но в противоположном направлении (как показано на рисунке), результат:
Поскольку результат равен 0, это означает, что векторы сбалансированы друг с другом и, следовательно, тело находится в равновесии или в состоянии покоя (оно не будет двигаться).
Разница между коллинеарным и параллельным векторами
Коллинеарные векторы характеризуются наличием одинакового направления на одной линии или потому, что они параллельны линии; то есть они являются векторами прямых параллельных линий.
С другой стороны, параллельные векторы определены, потому что они находятся в разных направлениях действия, которые перехвачены в одной точке.
Другими словами, они имеют одну и ту же точку отправления или прибытия – независимо от их модуля, направления или направления – образуя угол между ними.
Системы параллельных векторов решаются математическими методами или графами, которые являются методом параллелограмма сил и методом многоугольника сил. По ним будет определяться значение результирующего вектора, который указывает направление, в котором будет двигаться тело..
По сути, основное различие между коллинеарными векторами и параллельными векторами заключается в линии действия, в которой они действуют: коллинеарные действуют в одной линии, тогда как параллельные в разных.
То есть коллинеарные векторы действуют в одной плоскости: «X» или «Y»; и одновременный акт в обеих плоскостях, начиная с одной и той же точки.
Коллинеарные векторы не находятся в одной точке, как параллельные, потому что они параллельны друг другу.
На левом изображении вы можете увидеть блок. Он связан веревкой, а узел делит его на две части; когда тянуть в разные стороны и с разными силами, блок будет двигаться в том же направлении.
Представлены два вектора, которые совпадают в точке (блоке), независимо от их модуля, смысла или направления.
Вместо этого на правом изображении появляется шкив, который поднимает коробку. Веревка представляет собой линию действий; когда его тянут, на него действуют две силы (векторы): одна сила натяжения (при подъеме на блок) и другая сила, та, которая воздействует на вес блока. Оба имеют одинаковое направление, но в противоположных направлениях; не соглашайтесь в точке.
Источник статьи: http://ru.thpanorama.com/articles/matemticas/vectores-colineales-sistema-y-ejemplos.html
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Источник статьи: http://ru.onlinemschool.com/math/library/vector/colinearity/